Answer:
Bullet will hit the ground after 70 seconds.
Explanation:
A bullet is fired straight up from a BB gun with initial velocity 1120 ft/s at an initial height of 8 ft.

We need to find time when bullet hit the ground.
As we know when bullet hit the ground height would be 0
So, we set h=0 and solve for t .

Using quadratic formula
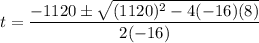
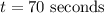
Thus, Bullet will hit the ground after 70 seconds.