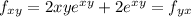Question

Calculate all four second-order partial derivatives and confirm that the mixed partials are equal. f(x,y)= 2e^xy

Answer 1

ANSWER TO QUESTION 1

The given function is


`f(x,y)=2 {e}^(xy)`

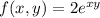
The partial derivative of f with respect to x means we are treating y as a constant. The first derivative is


`f_(x) = 2y {e}^(xy)`

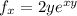
and the second derivative with respect to x is,


`f_(xx) = 2 {y}^(2) {e}^(xy)`

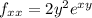
ANSWER TO QUESTION 2

The given function is


`f(x,y)=2 {e}^(xy)`

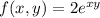
The partial derivative of f with respect to y means we are treating x as a constant. The first derivative is


`f_(y) = 2x{e}^(xy)`

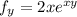
and the second derivative with respect to y is


`f_(yy) = 2 {x}^(2) {e}^(xy)`

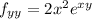
ANSWER TO QUESTION 3

Our first mixed partial is


`f_(xy)`

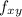
We need to differentiate

`f_(x) = 2y {e}^(xy)`
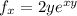
again. But this time with respect to y.

Since this is a product of two functions of y, we apply the product rule of differentiation to obtain,


`f_(xy) = 2y( {e}^(xy))' + ({e}^(xy))(2y)'`


`f_(xy) = 2xy {e}^(xy) + 2{e}^(xy)`

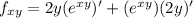
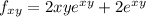
ANSWER TO QUESTION 4

The second mixed partial is


`f_(yx)`

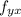
We need to differentiate

`f_(y) = 2x{e}^(xy)`

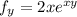
again. But this time with respect to x.

Since this is a product of two functions of x, we apply the product rule of differentiation to obtain,



`f_(yx) = 2x({e}^(xy))' + ({e}^(xy))(2x)'`


`f_(yx) = 2xy {e}^(xy) + 2{e}^(xy)`

Hence,


`f_(xy) = 2xy {e}^(xy) + 2{e}^(xy) =f_(yx)`