Question

Cos G =
5/12
12/13
5/13
12/5

Answer 1

`\boxed {\boxed {\sf cos(G)=(5)/(13) }}`

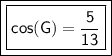
Explanation:

First, recall the trigonometric ratios.

• sin(θ)=opposite/hypotenuse
• cos(θ)= adajcent/hypotenuse
• tan(θ)=opposite/adjacent

The question asks us to find the cosine of G. Therefore, we need the adjacent side and the hypotenuse.

• Adjacent: 5 is the side next to angle G (12 is opposite, but we don't need that for cosine).
• Hypotenuse: 13 is the hypotenuse because it is the largest side and opposite the right angle.

Substitute the values into the ratio.

`cos(G)= (adjacent)/(hypotenuse)`

`cos(G)=(5)/(13)`

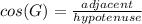
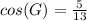
This fraction cannot be reduced further, so it is the answer.

The cosine of G is 5/13