For which of the following compound inequalities is there no solution?

Question

asked Oct 9, 2019 52.4k views

1 Answer

Eirikvaa · Answer 1 · 2019-10-12T15:44:20+0000

Answer:

The correct option is 1.

Explanation:

On solving both equations of option 1.

$4m\leq -32$

$m\leq -8$

From first equation the value of m is less than or equal to -8.

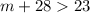
m+28>23

m>-5

From second equation the value of m is greater than -5. Therefore option have no common solutions.

On solving equation both equations of option 2, we get

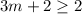
$3m+2\geq 2$

$m\geq 0$

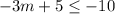
$-3m+5\leq -10$

$-3m\leq -15$

Divide both sides by -3. When we divide the inequality by a negative number, then we have to change the sign of inequality.

$m\geq 5$

Since m is greater than or equal to 0 and 5, therefore option 2 have common solution
$m\geq 5$ . So, the second option is incorrect.

On solving equation both equations of option 3, we get

-2m< 2

m>-1

11m>22

m>2

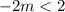
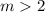
Since m is greater than -1 and 2, therefore option 3 have common solution
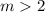m>2 . So, the third option is incorrect.

On solving equation both equations of option 4, we get

m+12< 8

m<-4

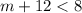
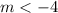
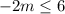
$-2m\leq 6$

$m\leq -3$

Since m is less than -4 and less than or equal to -3, therefore option 4 have common solution
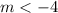m<-4 . So, the fourth option is incorrect.