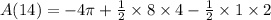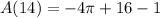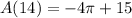Question

The graph of f is given in the figure to the right. Let ​A(x)equals=Integral from 0 to x f left parenthesis t right parenthesis font size decreased by 3 dt∫0xf(t) dt and evaluate ​A(4​), ​A(8​), ​A(12​), and ​A(14)

Answer 1

`A(4)=-4\pi`

`A(8)=-4\pi +8`

`A(12)=-4\pi +16`

`A(14)=-4\pi +15`

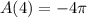
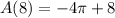
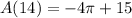
Explanation:

we are given

`A(x)=\int\limits^x_0 f{x} \, dx`

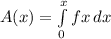
Calculation of A(4):

we can plug x=4

`A(4)=\int\limits^4_0 f{x} \, dx`

Since, this curve is below x-axis

so, the value of integral must be negative

and it is quarter of circle

so, we can find area of quarter circle

radius =4

`A(4)=-(1)/(4)* \pi * (4)^2`

`A(4)=-4\pi`

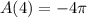
Calculation of A(8):

we can plug x=8

`A(8)=\int\limits^8_0 f{x} \, dx`

we can break into two parts

`A(8)=\int\limits^4_0 f{x} \, dx+\int\limits^8_4 f{x} \, dx`

now, we can find area and then combine them

`A(8)=-4\pi +(1)/(2)* 4* 4`

`A(8)=-4\pi +8`

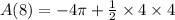
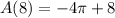
Calculation of A(12):

we can plug x=12

`A(12)=\int\limits^12_0 f{x} \, dx`

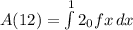
we can break into two parts

`A(12)=\int\limits^4_0 f{x} \, dx+\int\limits^8_4 f{x} \, dx+\int\limits^12_8 f{x} \, dx`

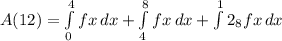
now, we can find area and then combine them

`A(12)=-4\pi +(1)/(2)* 8* 4`

`A(12)=-4\pi +16`

Calculation of A(14):

we can plug x=14

`A(14)=\int\limits^14_0 f{x} \, dx`

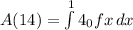
we can break into two parts

`A(14)=\int\limits^4_0 f{x} \, dx+\int\limits^8_4 f{x} \, dx+\int\limits^12_8 f{x} \, dx+\int\limits^14_12 f{x} \, dx`

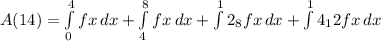
now, we can find area and then combine them

`A(14)=-4\pi +(1)/(2)* 8* 4-(1)/(2)* 1* 2`

`A(14)=-4\pi +16-1`

`A(14)=-4\pi +15`