Question

Perform the indicated goodness-of-fit test.

​Among the four northwestern states, Washington has 51% of the total population, Oregon has 30%, Idaho has 11%, and Montana has 8%. A market researcher selects a sample of 1000 subjects, with 450 in Washington, 340 in Oregon, 150 in Idaho, and 60 in Montana. At the 0.05 significance level, test the claim that the sample of 1000 subjects has a distribution that is consistent with the distribution of state populations. Select the correct conclusion about the null hypothesis.


Reject the null hypothesis. There is not sufficient evidence to warrant rejection of the claim that the distribution of the sample is consistent with the distribution of the state populations.


Fail to reject the null hypothesis. There is not sufficient evidence to warrant rejection of the claim that the distribution of the sample is consistent with the distribution of the state populations.


Reject the null hypothesis. There is sufficient evidence to warrant rejection of the claim that the distribution of the sample is consistent with the distribution of the state populations.


Fail to reject the null hypothesis. There is sufficient evidence to warrant rejection of the claim that the distribution of the sample is consistent with the distribution of the state populations.

Answer 1

Answer: Reject the null hypothesis. There is sufficient evidence to warrant rejection of the claim that the distribution of the sample is consistent with the distribution of the state populations.

Explanation:

The null and alternative hypotheses are:

`H_(0):`The sample of 1000 subjects has a distribution that is consistent with the distribution of state populations.

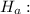`H_(a):`The sample of 1000 subjects does not have a distribution that is consistent with the distribution of state populations.

Under the null hypothesis, the test statistic is:

`\chi^(2)=\sum ((O-E)^(2))/(E)`

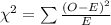
From the attachment, we clearly see the chi-square statistic is:

`\chi^(2)=31.938`

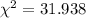
Now we have to find the chi-square critical value at 0.05 significance level for df = n - 1 = 4-1=3. Using the chi-square distribution table, we have:

`\chi^(2)_(critical) =7.815`

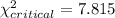
Since the chi-square statistic is greater than the chi-square critical value, we therefore reject the null hypothesis and there is sufficient evidence to warrant rejection of the claim that the distribution of the sample is consistent with the distribution of the state populations