Question

The points (-6, -3), (k,1) and (8,4) are collinear. Determine the value of k

Answer 1

The points are collinear, meaning that they are on the same line. Let's try to find the equation of the line. Since we have two points, we can use the point-slope form to find the equation, which is the following:

`(y - y_1) = m(x - x_1)`

• 
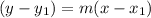
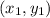  `(x_1, y_1)` is a point on the line
• 
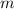  `m` is the slope of the line

First, let's find
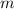`m`, the slope of the line. We are going to need to use the slope formula, which is the following:

`m = (y_2 - y_1)/(x_2 - x_1)`

• 
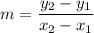
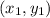  `(x_1, y_1)` and
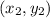  `(x_2, y_2)` are points on the line

Applying this to our problem, we can find the slope:

`m = (4 - (-3))/(8 - (-6)) = (7)/(14) = (1)/(2)`

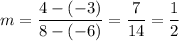
Now, let's find the equation of our line:

`(y - 4) = (1)/(2) (x - 8)`

`y = (1)/(2)x`

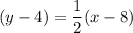
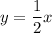
Now, let's set the equation of the line equal to 1, since we are trying to find the x-value that produces a y-value of 1.

`(1)/(2) x = 1`

`x = 2`

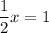
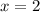
The answer is k = 2.