Answer:
a). x to the power of negative 2 multiplied by y to the power of negative 6, the whole over x to the power of 8 multiplied by y to the power of negative 8
Explanation:
Given
x multiplied by y to the power of 3 over x to the power of negative 4 multiplied by y to the power of 4, the whole to the power of negative 2.
Solving we get,

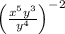
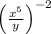

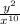
Now solving option A, we get
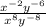
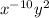
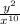
Hence proved, both are equal.
Option A is the answer.