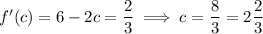We need to first check that
 is continuous on the interval
is continuous on the interval
![[0,3]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/ui0vb57kb247mvqkxsv63i89zp7q4s1prp.png) . If not, we're done. For this to happen, we need to have
. If not, we're done. For this to happen, we need to have

By the definition of
 ,
,
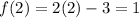 . The limits are then
. The limits are then
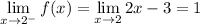
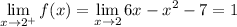
The function is indeed continuous.
Next, we check for differentiability. For the derivative to exist everywhere, we need it to be continuous too. So we compute the derivatives of the pieces (note the strict inequalities):
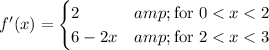
Judging by the first piece, in order for
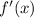 to be continuous on
to be continuous on
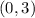 , the second piece must approach 2 as
, the second piece must approach 2 as
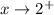 , and if this happens, we can safely conclude that
, and if this happens, we can safely conclude that
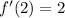 . We have
. We have
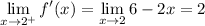
and so
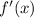 is indeed continuous, and hence
is indeed continuous, and hence
 is differentiable.
is differentiable.
Finally, we need to find the value(s) of
 between 0 and 3 (exclusive) such that
between 0 and 3 (exclusive) such that
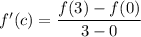
Since
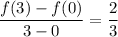 , and
, and
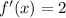 for
for
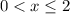 , we can expect
, we can expect
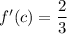 for some
for some
 between 2 and 3:
between 2 and 3: