Explanation:
Given : AD=CD and
∠3=∠4
To prove : Line DB bisects ∠ABC
i.e.∠ABD=∠CBD
Proof : Consider ΔABD and ΔCBD,
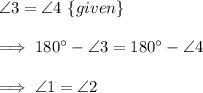
and
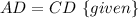
and
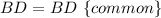
So, ΔABD ≅ ΔCBD (By SAS criterion}
Hence , By CPCT (corresponding part of congruent triangle}
∠ABD=∠CBD
Therefore, Line DB bisects ∠ABC.