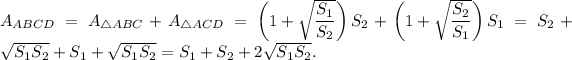Answer:
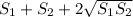
Explanation:
Consider trapezoid ABCD. Let triangle BEC be of area
 and triangle AED be of area
and triangle AED be of area
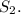
Triangles BEC and AED are similar with the coefficient of similarity
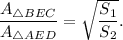
Consider triangles ABC and ACD. The area of these triangles are
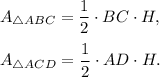
Note that
 where
where
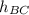 is the height of the triangle BEC,
is the height of the triangle BEC,
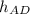 is the height of the triangle AED and
is the height of the triangle AED and
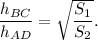
Thus,
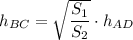 and
and
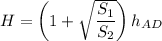 or
or
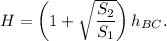
Then
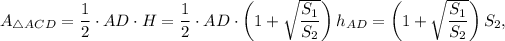
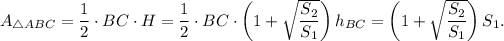
Thus, the area of trapezoid ABCD is