First, we want the fractions in the numerator to have the same denominator.
Find the LCM (least common multiple) of 5 and 10:
Multiples of 5: 5, 10, 15, 20
Multiples of 10: 10, 20
10 < 20
The LCM is 10. Divide the LCM by the smaller denominator for 2/5:
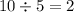
Multiply the numerator and denominator of the fraction by this number:
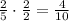
We can now solve for the overall numerator:
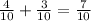
The expression should now look like this:
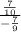
We can multiply the numerator by the fraction's denominator within the expression's denominator:
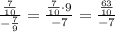
We can eliminate the denominator of the expression's numerator fraction by multiplying it by the expression's denominator:
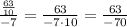
Find the GCF (greatest common factor) between 63 and 70:
Factors of 63: 1, 3, 7, 9, 21, 63
Factors of 70: 1, 2, 5, 7, 10, 14, 35, 70
7 > 1
GCF : 7
Divide the numerator and denominator by the GCF:
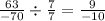
There is a negative sign in the denominator. Move this negative sign outside of the fraction:
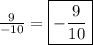
The answer in simplest form will be -9/10.