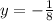For a parabola in the form of
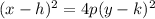 , the formula for the Focus and Directrix are as follows:
, the formula for the Focus and Directrix are as follows:
Focus is given by
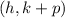 , and
, and
Directrix is given by
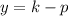 .
.
Let's rearrange the given equation in the form we want.
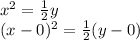 Where
Where

From this we can easily see that
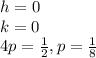 .
.
So from the formulas given above, we can see:
Focus is
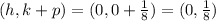 and
and
Directrix is
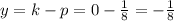 . So
. So
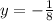
ANSWER: Focus is
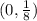 and Directrix is
and Directrix is