Answer : option D
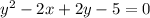
We apply completing the square method
Move all the y terms on one side
y^2 +2y = 2x + 5
In completing the square method , we take coefficient of y then divide it by 2 and square it
2/2 =1 then 1^2 = 1
Add it on both sides
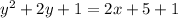
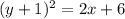
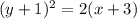
Solve for x
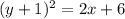
 (divide by 2 on both sides)
(divide by 2 on both sides)
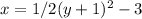
Vertex is (h,k) that is (-3,-1). h= -3 and k = -1
The value of a= 1/2

Plug in 1/2 for 'a'
so P = 1/2
Focus = (h+p, k)
h= -3 and k = -1, p = 1/2

Directrix x=(h - P)
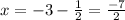
Option D is correct