Question

I need help with some Calculus Problems. I don't want the answer, I just want to know what steps I need to take to solve the problem.

1. If f(3)=
`(5pi)/(3)` and f'(3)=
`√(3)`, find the equation of the line tangent to g(x)= cos(f(x)) at x=3.


2. If f(x)=
`\sqrt{tan(2x+(3pi)/(4))}`, find
`lim_{x-\ \textgreater \ [tex](pi)/(4)`}[/tex] (f(x)-f(
`(pi)/(4)`))/(x-
`(pi)/(4)`)


Thank you.

Answer 1

1. we need to find g(3) and g'(3) to write point slope form of the tangent line

g(3)=cos(f(3))=
`cos((5 \pi)/(3))=(1)/(2)`

now to find g'(3)

use chain rule

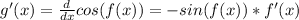`g'(x)=(d)/(dx)cos(f(x))=-sin(f(x))*f'(x)` so

`g'(3)=-sin(f(3))*f'(3)=-sin((5 \pi)/(3))*√(3)=`
`((√(3))/(2))(√(3))=(3)/(2)`

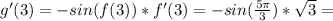
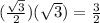
the equation of a line that passes through (x1,y1) and having a slope of m is

`y-y_1=m(x-x_1)`

we know it passes through (3,1/2) and has a slope of 3/2

so the equation of the tangent line at x=3 is

`y-(1)/(2)=(3)/(2)(x-3)`

2.ah, difference quotient

`\lim_{x \to (\pi)/(4)} (f(x)-f((\pi)/(4)))/(x-(\pi)/(4))=`

`\lim_{x \to (\pi)/(4)} \frac{\sqrt{tan(2x+(3 \pi)/(4))}-\sqrt{tan(2((\pi)/(4))+(3 \pi)/(4))}}{x-(\pi)/(4)}=`

`\lim_{x \to (\pi)/(4)} \frac{\sqrt{tan(2x+(3 \pi)/(4))}-1}{x-(\pi)/(4)}=`

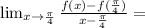
I don't know how to simplify further