Answer:
A and C is correct.
Explanation:
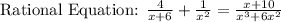
First we simplify this equation (-1 + x^2)/(x (6 + x))
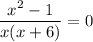
Solution set: x=1,-1
We have to check all option which is solution of above equation.
A) x=1, we will put x=1 into equation both sides.
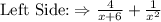
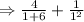

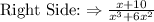
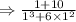


Thus, x=1 is a solution.
C) x=-1, we will put x=-1 into equation both sides.
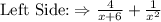

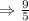


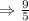
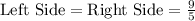
Thus, x=-1 is a solution.
Thus, A and C is correct.