Question

Given: FPST is a trapezoid, FP=ST, m∠F=45°, PF=8, PS=10

Find: The midsegment MN.

Answer 1

`4√(2)+10`

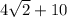
Explanation:

In trapezoid FPST, FP=ST, then this trapezoid is isosceles, so

`m\angle F=m\angle T=45^(\circ).`

Draw the height PH. Triangle FPH is right triangle with two angles of measure 45°. This means that FH=HP. By the Pythagorean theorem,

`FH^2+PH^2=PF^2,\\ \\2FH^2=8^2,\\ \\FH^2=32,\\ \\FH=4√(2).`

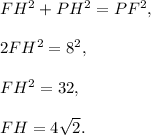
Since trapezoid FPST is isosceles, the base FT hasthe length

`FT=2FH+PS=8√(2)+10.`

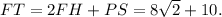
Then the length of the midline is

`MN=(FT+PS)/(2)=(8√(2)+10+10)/(2)=4√(2)+10.`