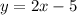Answer:
1. What is the slope of the line in the graph show below?
The line intercepts points (0,3) and (1,1).
We can find the slope using its formula

Therefore, the slope is -2. The right answer is A.
2. Find the slope of a line that passes through (-2,-3), and (1,1).
To find the slope, we apply the same formula as we did in the first question
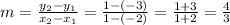
Therefore, the slope is 4/3.
3. For the equation -4y = 8x, what is the constant of variation?
To find the constant of variation, we need to express the given linear equation in the form
 . That is, we need to isolate
. That is, we need to isolate

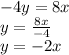
Where
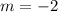 and
and
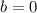 .
.
Therefore, the constant of variation is -2.
4. Suppose y varies directly with x, and y = 24 when x = 8. What is the value of y when x = 10?
This problem is setting a proportionality, that is, the raltion between the first pair of coordinates is the same for the second pair.
So, if y = 24 when x = 8, that means y-values are triple than x-values, because 8x3 = 24.
Now, if x = 10, then y = 3x10 = 30.
Therefore, the missing value is y = 30.
5. What is an equation for the line with slope 2/3 and y-intercept 9?
To find the equation, we use the slope-intercept formula

Where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.
In this case, we have
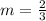 and
and
 .
.
Replacing these values, we have
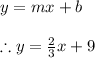
6. What is an equation in slope-intercept form for the line that passes through the points (1,-3) and (3,1)?
First, we need to find the slope
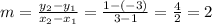
Then, we use the point-slope formula

Therefore, the slope-intercept form is