Question

What radical is 2^3/2 equal to?

Answer 1

Remember the following, which will help with this subject:

`x^(m)/(n) = \sqrt[n]{x^m}`

Using this property, we can say the following:

`2^(3)/(2) = √(2^3) = √(8)`

The answer is
`\boxed{√(8)}`.

Answer 2

`√(2^3)=2√(2)`.

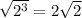Explanation:

We are asked to write
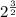`2^{(3)/(2)` as a radical.

We will use exponent property for radicals
`\sqrt[n]{a^m}=a^{(m)/(n)}` to rewrite our expression as a radical.

We can see that value of a is 2, value of m is 3 and value of n is 2, so our given expression as a radical would be:

`2^{(3)/(2)}=\sqrt[2]{2^3}`

`2^{(3)/(2)}=√(2^3)`

`2^{(3)/(2)}=√(2^2\cdot 2)`

`2^{(3)/(2)}=2√(2)`

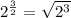
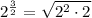
Therefore, our required radical is
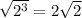`√(2^3)=2√(2)`.