Question

What is the average rate of change of y with respect to x over the interval [–2, 5] for the function y = 3x + 2?

Answer 1

Explanation:

Given the function: y=f(x) = 3x+2

when x=-2 at the beginning of the interval [-2, 5],

then;

y = 3x+2 begins at

y= 3(-2)+2 = -6+2= -4.

and

when x=5 at the end of the interval [-2, 5],

y = 3x+2 ends up at

y= 3(5)+2 = 15+2= 17.

So,

y has changed -4 to 17, which is a change of 17-(-4)= 17+4 = 21

and x has changed from -2 to 5, which is a change of 5-(-2)=5+2=7

So, the average rate of change of y with respect to x over the interval

[-2, 5] is given by ;

`(change of y over the interval)/(change of x over the interval)` =
`(21)/(7) = 3`

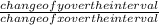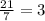
Therefore, the average rate of change y with respect to x over the interval is, 3