Question

Which graph represents the solution to the system of inequalities?

x + y ≤ 4

y – x ≥ 1

Answer 1

The solution to the system of inequalities can be represented by the shaded region where the two graphs overlap.

Step-by-step explanation:

The solution to the system of inequalities x + y ≤ 4 and y – x ≥ 1 can be represented by the shaded region where the two graphs overlap. To determine the graph, we need to rewrite the inequalities in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept.

For the first inequality, x + y ≤ 4, we can rewrite it as y ≤ -x + 4. This inequality represents a line with a slope of -1 and a y-intercept of 4.

For the second inequality, y – x ≥ 1, we can rewrite it as y ≥ x + 1. This inequality represents a line with a slope of 1 and a y-intercept of 1.

The graph of the system of inequalities is the shaded region where the two lines intersect.

Answer 2

Given inequalities are

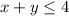`x+y\le4` and

`y-x\ge1`

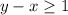
Now we will graph both inequalities to get the common region which represents solution.

Work for
`x+y\le4`

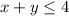
first we graph the line x+y=4 then shade the graph for inequality symbol
`\le`

we can plug any random number for x and find y-value to get points

lets plug x=0 then we get:

x+y=4

0+y=4

y=4

so the point is (0,4)

Similarly we can find more point like (4,0).

Now graph both points and join both points by straight line.

Now we find direction of shading.

pick any test point which is not on that line x+y=4 say (0,0)

and plug it into orinal inequality
`x+y\le4`

`0+0\le4`

`0\le4`

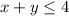
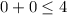
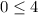
which is true.

True means shade in direction of test point. Otherwise we shade in opposite direction.

We will repeat same process for other inequality to graph that.

Hence final graph for the answer will be as shown in attached image.

Triangular region ABC is final answer.