Question

Find a polynomial function with real coefficients of degree 4 And zeros x=1-i and x=√(7). Let the leading coefficient be equal to 1. Written in factored form over rational numbers.

Answer 1

`p(x)=(x^(2) -2x+2)(x^(2) -7)`

Explanation:

Given that one of the zeroes is 1 - i.

Complex roots occur in pairs.

This means, if a + bi is a zero of a polynomial, then a - bi is also its zero.

Therefore, 1 + i is also a zero of the polynomial.

Factors are x - (1 - i) and x - (1 + i).

Multiply the factors.

[x - (1 - i)][x - (1 + i)] = (x - 1 + i)(x - 1 - i)

`=(x-1)^(2) -i^(2)`

`=(x-1)^(2) +1`

`=x^(2) -2x+1+1`

`=x^(2) -2x+2`

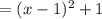
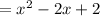
Given that one of the zeroes is
`√(7)`.

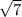Irrational roots occur in pairs.

This means, if an irrational number m is a zero of a polynomial, then - m is also its zero.

Therefore,
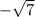`-√(7)` is also a zero of the polynomial.

Factors are
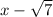`x-√(7)` and
`x+√(7)`.

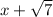Multiply the factors.

`(x-√(7) )(x+√(7) )`

`=x^(2) -√(7) ^(2)`

`=x^(2) -7`

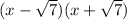
Hence, the required polynomial is
`p(x)=(x^(2) -2x+2)(x^(2) -7)`.