Question

One positive number is 14 less than another positive number. If the reciprocal of the smaller number is added to five times the reciprocal of the larger​ number, the sum is one fourth. Find the two numbers.

Answer 1

Let's call the two numbers
`s` and
`l`.

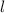Given these variables, we can say:
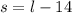`s = l - 14`, based on the first sentence in the problem.

Also, remember that the reciprocal of a number is simply 1 divided by the number. Thus, we can say that:

`(1)/(s) + 5\Big( (1)/(l) \Big) = (1)/(4)`

To solve, we can simply substitute
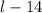`l -14` in for
`s` in the second equation and solve.

`(1)/(l - 14) + (5)/(l) = (1)/(4)`

• Set up

`(l)/(l(l - 14)) + (5(l - 14))/(l(l - 14)) = (1)/(4)`

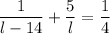
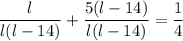
• Get terms on the left side to a common denominator for easier addition

`(l + 5l - 70)/(l(l - 14)) = (1)/(4)`

• Simplify

`4(6l - 70) = l(l - 14)`

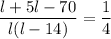
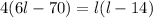
• Cross multiplication (
  `(a)/(b) = (c)/(d) \Rightarrow ad = bc`)

`24l - 280 = l^2 - 14l`

• Simplify

`l^2 - 38l + 280 = 0`

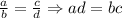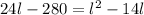
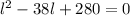
• Subtract
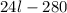  `24l - 280` from both sides of the equation

`(l - 10)(l - 28) = 0`

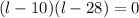
• Factor left side of the equation

`l = 10, 28`

• Zero Product Property

Now, notice that we have found two solutions, but the problem is only asking for one. This likely means that one of our solutions is extraneous. Let's take a look. Remember that the smaller positive number is equal to 14 less than the larger number. However,

`s = 10 - 14 = -4`,

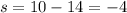Since
`s` is not positive in this case,
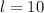`l = 10` is not a solution.

Thus,
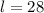`l = 28` is our only solution. In this case,

`s = 28 - 14 = 14`,

which means that the smaller number is 14 and the larger number is 28.