Question

1.Simplify.

2.Simplify.
3.Which statement best reflects the solution(s) of the equation?

Answer 1

Answer to question 1

We want to simplify

`((4x)/(5+x))/((6x)/(x+2))`

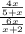
Let us change the middle bar to a normal division sign by rewriting the expression to obtain,

`(4x)/(5+x) / (6x)/(x+2)`

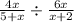
We now multiply the first fraction by the reciprocal of the second fraction to get,

`(4x)/(5+x) * (x+2)/(6x)`

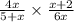
We cancel out common factors to obtain,

`(2)/(5+x) * (x+2)/(3)`

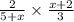
We multiply out to obtain,

`(2(x+2))/(3(x-5))`

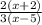
ANSWER TO QUESTION 2

We want to simplify,

`((x^2+4x+3)/(2x-1))/((x^2+x)/(2x^2-3x+1))`

Let us change the middle bar to a normal division sign by rewriting the expression to obtain,

`(x^2+4x+3)/(2x-1)/ (x^2+x)/(2x^2-3x+1)`

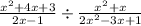
We now multiply the first fraction by the reciprocal of the second fraction to get,

`(x^2+4x+3)/(2x-1)* (2x^2-3x+1)/(x^2+x)`

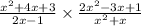
We now factor to obtain,

`((x+1)(x+3))/(2x-1)* ((x-1)(2x-1))/(x(x+1))`

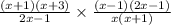
We now cancel out common factors to obtain,

`((x+3))/(1)* ((x-1))/(x)`

We now multiply out to get,

`((x-1)(x+3))/(x)`

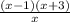
ANSWER TO QUESTION 3

We want to solve the equation,

`(1)/(x-1)+(2)/(x)=(x)/(x-1)`

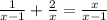
We need to multiply through by least common multiple of the denominators which is ,

`x(x-1)`

`x(x-1) * (1)/(x-1)+x(x-1) * (2)/(x)=x(x-1) * (x)/(x-1)`

`x+2(x-1)=x(x)`

`x+2x-2=x^2`

`3x-2=x^2`

`x^2-3x+2=0`

`(x-1)(x-2)=0`

`x=1,x=2`

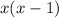
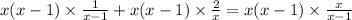
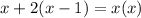
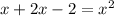
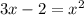
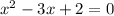
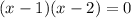
But
`x=1` does not satisfy the equation. It will result in division by zero which is undefined. This is an extraneous solution.

Therefore
`x=2` is the only solution.

The correct answer is D.