Question

The coordinates below represent two linear equations. How many solutions does this system of equations have? Line 1 x y –3 6 3 4 Line 2 x y –6 7 9 2 A. 0 B. exactly 1 C. exactly 2 D. infinitely many

Answer 1

A. Many solution

Step by step explanation

Points on line 1 : (-3, 6) and (3, 4)

Points on line 2: (-6, 7) and (9, 2)

Now let's find the slope of the line 1

Slope formula =
`(y2 - y1)/(x2 - x1)`

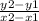
Slope of line 1 = (4 - 6) / (3 - (-3)

= -2/(3 + 3)

= -2/6

Slope of line 1 = -1/3

The equation of the line y - y 1 = m(x - x1)

y - 6 = -1/3 (x - (-3))

y -6 = -1/3 (x + 3)

y -6 = -1/3x - 1

y = -1/3x + 5

Slope of line 2 = (2 - 7) / (9 -(-6))

= -5/(9 + 6)

= -5/15

Slope of line 2 = -1/3

The equation of line

y - y1 = m(x - x1)

y - 7 = -1/3(x - (-6))

y - 7 = -1/3(x + 6)

y -7 = -1/3 x - 2

y = -1/3 x + 5

The line 1 and line 2 have the same slopes and the same y-intercept. Both are the same equation. Therefore, there will be many solution.

Answer : A. 0 Solution

Thank you.