Question

a carnival game consists of 3 dart throws at a target. The probability of scoring a hit on any one throw is 30%. Using the binomial formula, find the probability of scoring 2 hits.

Answer 1

Answer: Probability of scoring 2 hits = 0.63.

Explanation:

Since we have given that

Number of dart throws at a target = 3

Probability of scoring a hit on any one throw = 30%

We will use "Binomial Distribution" i.e.

`P=^nC_rp^r(1-p)^(n-r)`

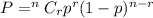
where,

n denotes number of dart throws at a target,

r denotes number of required throws

p denotes probability of success

(1-p) denotes probability of failure

So, Probability of success is given by

`(30)/(100)=(3)/(10)`

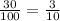
Probability of failure is given by

`1-(30)/(100)=(70)/(100)=(7)/(10)`

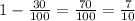
We will use "Binomial Distribution" i.e.

`P(X=2)=^3C_2((3)/(10))^2* ((7)/(10))\\\\P(X=2)=(9)/(100)* (7)/(100)\\\\P(X=2)=(63)/(100)\\\\P(X=2)=0.63`

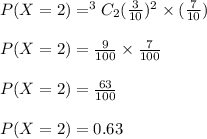
Hence, Probability of scoring 2 hits = 0.63.