B
given the equation of a parabola in standard form
y = ax² + bx + c : a ≠ 0
then the equation of the axis of symmetry which is also the x- coordinate of the vertex is obtained using
x = -
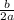
y = 4x² + 5x - 1 is in standard form
with a = 4, b = 5 and c = - 1
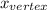 = -
= -
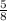
hence axis of symmetry is x = -
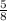
to find the y-coordinate of the vertex substitute the x-coordinate into the equation
y = 4(-
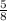 )² + 5(-
)² + 5(-
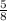 ) - 1
) - 1
=
 -
-
 -
-
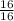
= -
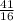 = - 2
= - 2
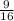
vertex = ( -
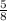 , - 2
, - 2
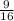 )
)