Question

Kristen invests $5,745 in a bank. The bank pays 6.5% interest compounded monthly. How long must she leave the money in the bank for it to double? Round the nearest tenth of a year.

Answer 1

formula is
`A=P(1-(r)/(n))^(nt)`

where A=final amount

P=principal

r=interest rate in decimal

n=number of times per year it is compounded

t=time in years

we want to find where

A=2P

and P=5745

and r=6.5%=0.065

n=monthly=12

remember that
`ln(x^a)=a(ln(x))`

also that
`(a^b)^c=a^(bc)`

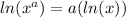
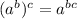
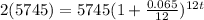`2(5745)=5745(1+(0.065)/(12))^(12t)`, solving for t

divide both sides by 5745 to simplify things a bit

`2=(1+(0.065)/(12))^(12t)` I'd rather not simplify this because it give us a decimals and those aren't exact, if we combine, we get 12.065/12 for inside parenthases

`2=((12.065)/(12))^(12t)`

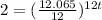
take ln of both sides

`ln(2)=ln(((12.065)/(12))^(12t))`

`ln(2)=(12t)ln((12.065)/(12))`

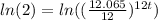
divide both sides by
`12ln((12.065)/(12))`

`(ln(2))/(12ln((12.065)/(12)))=t`

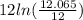
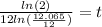
using our calculator, t≈10.6927

so rounded, we get 10.7 years