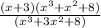Question

The volume of a rectangular prism is (x4 + 4x^3 + 3x^2 + 8x + 4), and the area of its base is (x3 + 3x^2 + 8). If the volume of a rectangular prism is the product of its base area and height, what is the height of the prism?

Answer 1

`V=x^4+4x^3+3x^2+8x+4\\\\B=x^3+3x^2+8\\\\V=BH\to H=(V)/(B)\\\\\text{Substitute:}\\\\H=(x^4+4x^3+3x^2+8x+4)/(x^3+3x^2+8)`

Answer 2

Height =
`((x+3)(x^(3)+x^(2)+8))/((x^(3)+3x^(2)+8))`

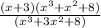
Explanation:

The volume of a rectangular prism =
`(x^(4)+4x^(3)+3x^(2)+8x+4)`

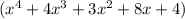
and the area of the base = (
`(x^(3)+3x^(2)+8)`

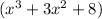
We know the formula,

Volume of the rectangular prism = Area of the base × Height

Height =
`\frac{\text{Volume of the prism}}{\text{Area of the base}}`

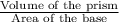
Now plug in the value of volume and area in the formula

Height =
`(x^(4)+4x^(3)+3x^(2)+8x+24)/(x^(3)+3x^(2)+8)`

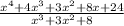
Further solving the fraction

Height =
`((x+3)(x^(3)+x^(2)+8))/((x^(3)+3x^(2)+8))`