Question

Give the excluded values for the rational equation.

(3x)/(x-4)-(x+3)/(x+4)=(2x+7)/(x^(2)-16)

Answer 1

Answer is x =-4 and x =4

Step-by-step explanation:

`(3x)/(x-4) -(x+3)/(x+4)=(2x+7)/(x^2-16)\\Let us take LCD\\(3x(x+3)-(x+3)(x-4))/(x^2-16)= (2x+7)/(x^2-16)`

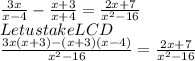
We find that there is a common denominator.

This should not be equal to 0.

i.e. x ≠4 or x ≠-4

Thus x=4 and x=-4 are the excluded values for the rational equation.

Once we exclude these values, we cancel and equate numerator

3x(x+4)-(x+3)(x-4) = 2x+7

Simplify to get 3x^2+12x-x^2+x-12 = 2x+7

2x^2+11x-19 =0

Thus when we exclude those values, we et a quadratic equation with 2 solutions.

simplify to get

Answer 2

`(3x)/(x-4)  - (x+3)/(x-4) = (2x+7)/(x^2-16)`

We factor the denominators

Factor x^2 - 16

x^2 - 4^2

We use a^2 - b^2 = (a+b)(a-b)

so x^2 - 4^2 = (x+4)(x-4)

Replace it in the given equation

`(3x)/(x-4)  - (x+3)/(x-4) = (2x+7)/((x+4)(x-4))`

Excluded values are the values that makes the denominator 0

we have (x-4) and (x+4) in the denominator

We set the denominator =0 and solve for x

x-4 =0

Add 4 on both sides

x= 4

x+4=0

subtract 4 onboth side

so x= -4

Excluded values are x=-4 and x=4