Question

Kristen invests $ 5745 in a bank. The bank 6.5% interest compounded monthly. How long must she leave the money in the bank for it to double? Round to the nearest tenth of a year. Show your work.

How long will it take to triple? Round to nearest tenth of a year. Show your work.
Kristen has a choice to invest her money at 6.5% interest compounded monthly for 5 years or invest her money compounding quarterly at a rate of 6.75% for 5 years. What option would be best for Kristen? Explain and show your work.

Answer 1

1. 10.7 years

2. 17.0 years

3. 2nd option

Explanation:

Use formula for compounded interest

`A=P\cdot \left(1+(r)/(n)\right)^(nt),`

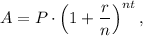
where

A is final value, P is initial value, r is interest rate (as decimal), n is number of periods and t is number of years.

In your case,

1. P=$5745, A=2P=$11490, n=12 (compounded monthly), r=0.065 (6.5%) and t is unknown. Then

`11490=5745\cdot \left(1+(0.065)/(12)\right)^(12t),\\ \\2=(1.0054)^(12t),\\ \\12t=\log_(1.0054)2,\\ \\t=(1)/(12)\log_ {1.0054}2\approx 10.7\ years.`

2. P=$5745, A=3P=$17235, n=12 (compounded monthly), r=0.065 (6.5%) and t is unknown. Then

`17235=5745\cdot \left(1+(0.065)/(12)\right)^(12t),`

`3=(1.0054)^(12t),`

`12t=\log_(1.0054)3,`

`t=(1)/(12)\log_(1.0054)3\approx 17.0\ years.`

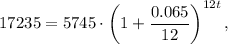
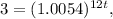
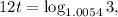
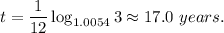
3. 1 choice: P=$5745, n=12 (compounded monthly), r=0.065 (6.5%), t=5 years and A is unknown. Then

`A=5745\cdot \left(1+(0.065)/(12)\right)^(12\cdot 5),\\ \\A=5745\cdot (1.0054)^(60)\approx \$7936.39.`

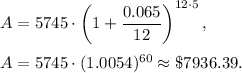
2 choice: P=$5745, n=4 (compounded monthly), r=0.0675 (6.75%), t=5 years and A is unknown. Then

`A=5745\cdot \left(1+(0.0675)/(4)\right)^(4\cdot 5),\\ \\A=5745\cdot (1.0169)^(20)\approx \$8032.58.`

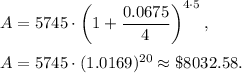
The best will be 2nd option, because $8032.58>$7936.39