Question

Write the equation in standard form for the circle that has a diameter with endpoints (0,8) and (0, - 8)

Answer 1

Hello!

Step-by-step explanation:

Slope-intercept form: →
`y=mx+b`

m: represents the slope and is constant.

b: represents the y-intercept.

Used rise/run.

`(rise)/(run)`

`Slope=(y^2-y^1)/(x^2-x^1)`

`(x^1,y^1)=(0,8)`

`(x^2,y^2)=(0,-8)`

`rise=y^2-y^1=-8-8=-16`

`run=x^2-x^1=0-0=0`

`=(-16)/(0)`

Undefined is -16/0

But the slope is -16

And the y-intercept is 0.

Hope this helps!

Answer 2

so the endpoints are at (0,8) and (0,-8) for the diameter, meaning half-way in between those points, is the center of the circle, and the distance of between those points, is the diameter, but half of that, is its radius.

so let's find the center of it and radius then.

`\bf ~~~~~~~~~~~~\textit{middle point of 2 points } \\\\ (\stackrel{x_1}{0}~,~\stackrel{y_1}{8})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-8}) \qquad \left(\cfrac{ x_2 + x_1}{2}~~~ ,~~~ \cfrac{ y_2 + y_1}{2} \right) \\\\\\ \left( \cfrac{0+0}{2}~,~\cfrac{-8+8}{2} \right)\implies (0,0)`

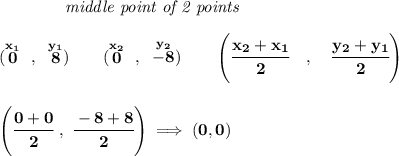
so the center is at the origin, now

`\bf ~~~~~~~~~~~~\textit{distance between 2 points} \\\\ (\stackrel{x_1}{0}~,~\stackrel{y_1}{8})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-8})\qquad \qquad d = √(( x_2- x_1)^2 + ( y_2- y_1)^2) \\\\\\ \stackrel{diameter}{d}=√((0-0)^2+(-8-8)^2)\implies d=√((-16)^2) \implies d=16 \\\\\\ \textit{so then the radius is half that }\cfrac{16}{2}\implies r=8 \\\\[-0.35em] \rule{34em}{0.25pt}`

`\bf \textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \qquad center~~(\stackrel{0}{ h},\stackrel{0}{ k})\qquad \qquad radius=\stackrel{8}{ r} \\\\\\ (x-0)^2+(y-0)^2=8^2\implies \boxed{x^2+y^2=64}`