Question

Which of the following combined with the equation −9x + 3y = 12 creates a system of linear equations with no solution?

Select one:
A.
18x - 6y = 20

B.
3x - y = -4

C. -16x + 9y = 30
D.
5x + 8y = -1

Answer 1

ANSWER

The correct answer is option A

Step-by-step explanation

A line that will create a system of equation with no solution when combined with

`- 9x + 3y = 12`
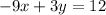
,is the line that has the same slope as

`- 9x + 3y = 12`
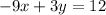
but different y-intercept.

So, let us write the given equation in slope intercept form to obtain,


`3y = 9x + 12`


`\Rightarrow \: y = 3x + 4`

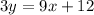
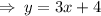
The slope is

`3`
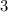
and y-intercept is

`4.`

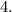
Now let us determine the slope and intercept for the given options too.

For option A,


`18x - 6y = 20`


`\Rightarrow \: - 6y = - 18x + 20`


`\Rightarrow \: y = 3x - (10)/(3)`

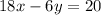
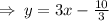
This has the same slope as the given equation but different y-intercept. When combined with the given equation, there will be no solution, since the two lines will never intersect. so it is the correct option.

For option B,


`3x - y = - 4`


`\Rightarrow \: -y = - 3x - 4`


`\Rightarrow \: y = 3x + 4`

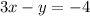
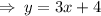
This option has the same slope and y-intercept as the given line so when combined with this equation, there will be infinitely many solution.

As for option C and D they do not have the same slope as the given line so there will be a unique solution when each is combined with the given line.