Question

IF AN8 COUNT PACK OF BUNS COST 0.03 CENTS MORE PER BUN THAN A PACK OF 10 COUNT BUNS , ANT THE 8 COUNT IS 0.45 CENTS LESS THAN THE 10 COUNT PACKAGE. HOW MUCH DOES THE 8 COUNT AND THE 10 COUNT PACKS COST

Answer 1

So,

Let's calm down and translate this word problem.

The 8-ct. pack costs 0.03 cents more per bun than the 10-ct. pack.

x = cost of 8-ct. pack

y = cost of 10-ct. pack

We now have the equation:

`(x)/(8)=(y)/(10)+0.03\ cents`

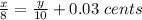
Also, we are told that the 8-ct. pack is 0.45 cents less than the 10-ct. pack.

x = y - 0.45 cents

With these two equations, we can now solve for x and y.

First, substitute y - 0.45 cents for x in the first equation.

`(y-0.45cents)/(8)=(y)/(10)+0.03\ cents`

Multiply both sides by 80 and simplify.

10(y - 0.45 cents) = 8y + 2.40 cents

10y - 4.50 cents = 8y + 2.40 cents

Subtract 8y from both sides and add 4.50 cents to both sides.

2y - 4.50 cents = 2.40 cents

2y = 6.90 cents

Divide both sides by 2.

y = 3.45 cents

Substitute 3.45 cents for y in the second equation.

x = 3.45 cents - 0.45 cents

x = 3.00 cents

The 8-ct. pack costs 3.00 cents, and the 10-ct. pack costs 3.45 cents.