For lines to be parallel, the slopes have to be the SAME.
To find the value of k, you can first find the slope of line 1 using the slope(m) formula, and plug in the points:
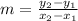
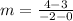
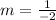
Now that you know the slope, you can use the slope formula to find k by plugging in what you know:
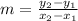
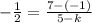 Multiply (5 - k) on both sides
Multiply (5 - k) on both sides
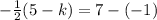 Multiply -2 on both sides
Multiply -2 on both sides
5 - k = -2(7 + 1)
5 - k = -2(8)
5 - k = -16 Subtract 5 on both sides
-k = -21 Divide -1 on both sides
k = 21