1. Balancing nuclear equations
Answer:
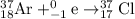
Explanation:
The main point to remember in balancing nuclear equations is that the sums of the superscripts (the mass numbers) and the subscripts (the nuclear charges) must balance.
Mass numbers: 37 + 0 = 37; balanced.
Charges: 18 + 1 = 17; balanced
B is wrong. Mass numbers not balanced. 6 +2(1) ≠ 4 + 3.
C is wrong. Mass numbers not balanced. 254 + 4 ≠ 258 + 2(1).
D is wrong. Mass numbers not balanced. 14 + 4 ≠ 17 + 2.
===============
2. Amount remaining
Answer:
D. 5.25 g
Explanation:
The half-life of Th-234 (24 da) is the time it takes for half the Th to decay.
After one half-life, half (50 %) of the original amount will remain.
After a second half-life, half of that amount (25 %) will remain, and so on.
We can construct a table as follows:
No. of Fraction Amount
half-lives t/(da) remaining remaining/g
1 24 ½ 21.0
2 48 ¼ 10.5
3 72 ⅛ 5.25
4 96 ¹/₁₆ 2.62
We see that 72 da is three half-lives, and the amount of Th-234 remaining is 5.25 g.
===============
3. Calculating the half-life
Answer:
a. 2.6 min
Explanation:
The fraction of the original mass remaining is 1.0 g/4.0 g ≈ ¼.
We saw from the previous table that it takes two half-lives to decay to ¼ of the original amount.
2 half-lives = 5.2 min Divide both sides by 2
1 half-life = 5.2 min/2 = 2.6 min