Question

The

lifting force, F, exerted on an airplane wing varies jointly as the area, A, of the wing's surface and the square of the plane's velocity, v. The lift of a wing with an area
of 180 square feet is 10,500 pounds when the plane is going 140 miles per hour. Find the lifting force on the wing if the plane speeds up to 230 miles per hour. (Leave
the variation constant in fraction form or round to at least 5 decimal places. Round off your final answer to the nearest pound.) could someone please help quick. I’m stumped

Answer 1

28,339 lbs

Explanation:

If the lifting force exerted on an airplane wing varies jointly as the area of the wing's surface and the square of the plane's velocity then:

`F \propto Av^2 \implies F=kAv^2`

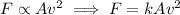
Where:

• F = lifting force in pounds (lbs)
• A = area in square feet (ft²)
• v = velocity in miles per hour (mph)
• k = some constant

Given:

• F = 10,500 lbs
• A = 180 ft²
• v = 140 mph

Substitute the given values into the found equation and solve for k (variation constant):

`\begin{aligned}F & = kAv^2\\\\10500 & = k \cdot 180 \cdot 140^2\\10500 & = 3528000k\\k & = (10500)/(3528000)\\\implies k & = (1)/(336)\end{aligned}`

Therefore:

`\boxed{ F=(1)/(336)Av^2}`

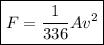
To find the lifting force (F) when the plane speeds up to 230 mph, substitute the given area of the wing (A = 180 ft²) and the new velocity (v = 230 mph) into the equation and solve for F:

`\begin{aligned}F&=(1)/(336)Av^2\\\implies F& = (1)/(336) \cdot 180 \cdot 230^2\\& = (1)/(336) \cdot 180 \cdot 52900\\& = (1)/(336) \cdot 9522000\\& = (9522000)/(336) \\& =28339.2857...\\&=28339\;\sf lbs \; (nearest\:pound)\end{aligned}`

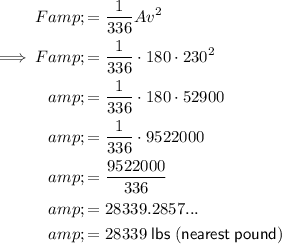
Therefore, the lifting force is 28,339 lbs (nearest pound).