Question

What is the value of y?

Enter your answer in the box

y =

An isosceles triangle A B C. Side B C is the base. Sides A B and A C are equal. Sides A B and A C are labeled with single tick marks. Angle A is labeled as left parenthesis 2 y plus 20 right parenthesis degrees, angle B is labeled as left parenthesis 5 x right parenthesis degrees, and angle C is labeled as 40

Answer 1

Answer: y= 40

Explanation:

Given : An isosceles triangle ABC.

∠A = (2y+20)°

∠B= (5x)°

∠C = 40°

Also, it is given that Sides AB and AC are equal.

⇒ ∠B = ∠C [∵ angles opposite to equal sides of a triangle are equal.]

⇒ ∠B = 40°

`\Rightarrow\ 5x=40\\\\\Rightarrow\ x= (40)/(5)=8`

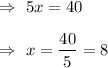
So the value of x= 8

Using Angle sum property of triangle , we have

∠A+∠B+ ∠C=180°

⇒ (2y+20)° +40°+40°=180°

⇒ 2y+20+ 40+40=180

⇒ 2y+100=180

⇒ 2y =180-100 =80

⇒ y =40 [divide both sides by 2]

Hence, the value of y= 40

Answer 2

The value of y = 40.

Explanation:

We have been given that Δ ABC is isosceles with AB = AC.

Since opposite angles of equal sides are equal, we have,

∠C = ∠B and so

5x = 40

x = 8

Now, by angle sum property,

∠A + ∠B + ∠C = 180⁰

(2y + 20) + 40 + 40 = 180

(2y + 20) + 80 = 180

(2y + 20) = 180 - 80

2y + 20 = 100

2y = 100 - 20 = 80

y = 40

Hence, the value of y = 40°.