Question

At a particular academically challenging high school, the average gpa of a high school senior is known to be normally distributed. after a sample of 20 seniors is taken, the average gpa is found to be 2.71 and the variance is determined to be 0.25. find a 90% confidence interval for the population mean gpa.

Answer 1

Solution: The 90% confidence interval for the population mean is:

`\bar{x} \pm t_{(0.1)/(2)} (s)/(√(n))`

Where:

`\bar{x}=2.71`

`s=√(0.25) =0.5`

`t_{(0.1)/(2)}=1.729` is the critical value at 0.1 significance level for df = n-1 =20-1=19

`2.71 \pm 1.729 (0.5)/(√(20))`

`2.71 \pm0.19`

`\left( 2.71-0.19,2.71+0.19\right)`

`\left(2.52,2.90 \right)`

Therefore, the 90% confidence interval for the population mean is
`\left(2.52,2.90 \right)`

Answer 2

The 90% confidence interval for the population mean gpa is [2.526,2.894].

Explanation:

The confidence interval for population mean is

`\mu\pm z^(*)\cdot (\sigma)/(√(n))`

Where, μ is population mean, σ is standard deviation, z* is the value of z-score and n is number of samples.

The z-score value for 90% confidence interval is 1.645.

The average gpa is found to be 2.71, so μ=2.71. The variance is 0.25, it means

`\sigma^2=0.25`

`\sigma=0.5`

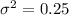
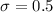
The 90% confidence interval for population mean is

`2.71\pm 1.645\cdot (0.5)/(√(20))`

`[2.71-1.645\cdot (0.5)/(√(20)),2.71+1.645\cdot (0.5)/(√(20))]`

`[2.526,2.894]`

Therefore the 90% confidence interval for the population mean gpa is [2.526,2.894].