Question

Which answer best describes the complex zeros of the polynomial function?

f(x)=x3−x2+6x−6




The function has two real zeros and one nonreal zero. The graph of the function intersects the x-axis at exactly one location.


The function has one real zero and two nonreal zeros. The graph of the function intersects the x-axis at exactly one location.


The function has one real zero and two nonreal zeros. The graph of the function intersects the x-axis at exactly two locations.


The function has three real zeros. The graph of the function intersects the x-axis at exactly three locations.

Answer 1

B.) The function has one real zero and two nonreal zeros. The graph of the function intersects the x-axis at exactly one location.

Step-by-step explanation:

Answer 2

Answer: The correct option is 2.

Step-by-step explanation:

The given polynomial is,

`f(x)=x^3-x^2+6x-6`

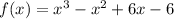
By rational root theorem 1 and -1 are possible roots of all polynomials.

put x=1

`f(x)=(1)^3-(1)^2+6(1)-6=0`

Since the value of f(x) is 0 at x=1. So 1 is a real root of the polynomial.

Divide the given polynomial by (x-1) using synthetic division method.

`f(x)=(x-1)(x^2+6)`

Equate each factor equal to 0.

`x=1`

`x=\pm√(-6)`

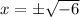
So, the given polynomial have one real root and 2 non real roots. Since the function have one real root therefore the function intersects the x-axis at exactly one location.

Thus, the correct option is 2.