Question

In a triangle ABC, AD is drawn perpendicular to BC.
Prove that AB2 - BD2 = AC2 - CD2.

Answer 1

Given: In triangle ABC , AD is drawn perpendicular to BC.

Since AD is drawn perpendicular to BC, it creates two right triangles: ADB and ADC.

Prove that:
`AB^2-BD^2 = AC^2-CD^2`

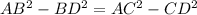
Pythagoras triangle for right angle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.

In a right angle triangle ADB;

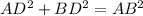`AD^2+BD^2 = AB^2` [By Pythagoras theorem]

or

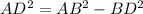`AD^2= AB^2-BD^2` .......[1]

Now, in right angle triangle ADC;

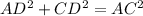`AD^2+CD^2 = AC^2` [By Pythagoras theorem]

or we can write this as;

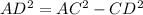`AD^2= AC^2-CD^2` ......[2]

Substituting the equation [1] in [2] we get;

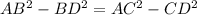`AB^2-BD^2 =AC^2-CD^2` hence proved!