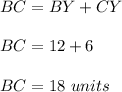Question

in the figure, square wxyz has a diagonal of 12 units. point a is a midpoint of segment wx, segment ab is perpendicular to segment ac and ab=ac. what is the length of segment bc?

Answer 1

Answer: BC= 18 units .

Step-by-step explanation:

Since we have given that

Diagonal of square WXYZ is given by

`12√(2)`

As we know the formula of "Diagonal of square",

`D=a\sqrt2\\\\12=a√(2)\\\\(12)/(√(2))=a\\\\6√(2)=a`

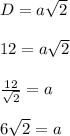
Since 'A' is the midpoint of WX so,

Length of AX=YE is given by

`(6√(2))/(2)=3√(2)`

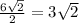
Since AB=AC and ΔABC is right angled triangle , so,

`\angle C=\angle B=45\textdegree(\text{ because equal sides have equal angles })`

So, In ΔCEY,

`sin(45\textdegree)=(EY)/(CY)\\\\(1)/(\sqrt2)=(3\sqrt2)/(CY)\\\\CY=3\sqrt2* \sqrt2=3* 2=6\ units`

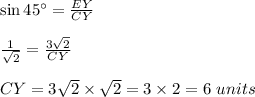
in ΔXYB,

`sin(45\textdegree)=(XY)/(BY)\\\\(1)/(\sqrt2)=(6\sqrt2)/(CY)\\\\CY=6\sqrt2* \sqrt2=6* 2=12\ units`

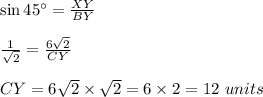
So,

`BC=BY+CY\\\\BC=12+6\\\\BC=18\ units`