Question

Write the standard form of the equation of a circle with a radius of 2 and center at (4,-5)

Answer 1

`(x-4)^2+(y+5)^2=4`

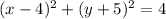
Explanation:

We are given a circle with a radius of 2 with a center at the point (4, -5).

Assuming x and y to be the coordinates of any point on the circle, we can find the equation of the circle by using the following distance formula:

`r=√((x_1-x)^2+(y_1-y)^2)`

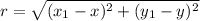
Putting the given values to get:

`2=√((x-4)^2+(y+5)^2)`

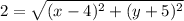
Taking square on both sides to get:

`4=(x-4)^2+(y+5)^2`

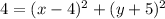
Therefore, the equation of the given circle with radius 2 and center at (4, -5) is
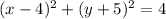`(x-4)^2+(y+5)^2=4`.

Answer 2

center-radius form of the circle (x – h)^2 + (y – k^)2 = r^2

(x-4)^2 + (y--5)^2 = 2^2

(x-4)^2 +(y+5)^2 = 4