Answer:
5
Explanation:
Given inequality,

For
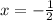

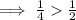 ( False )
( False )
For

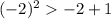
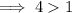 ( true )
( true )
For


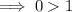 ( False )
( False )
For
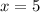
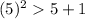
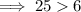 ( True )
( True )
Thus, x = -2 and 5 are the solutions of the given inequality,
But, negative numbers are not allowed.
Hence, x = 5 is a counterexample to kelvins conjecture.