Question

Assume that a procedure yields a geometric distribution where the probability of success is 63%. Use the geometric probability formula to find the probability that the first success occurs after the sixth trial.

0.003
0.014
0.055
0.125

Answer 1

Option A - 0.003

Explanation:

Given: Probability of success = 63%= 0.63

Probability of failure = 1-0.63=0.37

To find: Probability that the first success occurs after the sixth trial

Formula for calculating geometric probabilities:

If P(X >n) or the probability that it takes more than a certain number of trials to achieve the first success.

`P(X>n)=(1-p)^n`

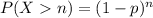
where, X has a geometric distribution,p is the probability of success and (1-p) is the failure and possible values of X are 1, 2, 3, ....

Now, put values p=0.63, (1-p)= 0.37 , n=6 in the formula

`P(X>n)=(1-p)^n`

`P(X>6)=(0.37)^6`

`P(X>6)=0.0025`

`P(X>6)=0.003`

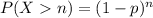
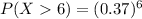
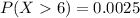
Therefore, Option A is correct