Answer:
C and D.
Explanation:
We are given that Spencer wrote a paragraph for proving that rectangles are parallelograms with congruent diagonals
We have to find the missing step in Spencer's proof
Proof:
According to the given information quadrilateral RECT is a rectangle. By definition of a rectangle , all four angles measure
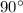
.Segment ER is parallel to segment CT and segment EC is parallel to segment RT by the converse of the same- side Interior Angles Theorem.
Converse of the same- side angles theorem: When the sum of same side interior angles of a transversal line is
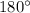 then the lines are parallel.
then the lines are parallel.
Quadrilateral RECT is then a parallelogram by definition of a parallelogram .Now, construct diagonals ET and CR. Because RECT is a parallelogram ,opposite sides are congruent.Therefore, one can say that segment ER is congruent to segment CT.Segment TR is congruent to itself by the reflexive Property of equality.The Side-Angle-Side(SAS) Theorem says triangle ERT is congruent to triangle CTR.And because corresponding parts of congruent triangles are congruent (CPCTC),diagonals ET and Cr are congruent.
Answer :Option C and D
Converse of the same-Side Interior angles Theorem