Question

Does each equation represent exponential decay or exponential growth?

Drag and drop the choices into the boxes to correctly complete the table.

Note: If an equation is neither exponential growth nor exponential decay, do not drag it to the table.

Answer 1

Exponential Decay:

W=9/8(3/5)^t

f(t)=(3/4)^t

L=4.2(0.6)^t

Exponential Growth:

L=0.25(12)^t

W=0.5(2.1)^t

f(t)=2/3(6)^t

Neither:

G(x)=1.3(x)

Answer 2

The best way to know if an equation represents an exponential growth or decay is to look a the base of the exponentiation.

If the base is larger than 1, it will be an exponential growth.

For example,
`3^(2) = 9`

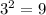
If the base is smaller than 1, it will be an exponential decay.

For example,
`0.5^(2) = 0.25`

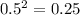
If the function does not have an exponent, that means there will be no exponential growth or decay.

Therefore:

Exponential Decay (base smaller than 1):

`W=(9)/(8)((3)/(5))^(t)`

`f(t)=((3)/(4)) ^t`

`L=4.2(0.6)^t`

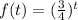
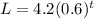
Exponential Growth (base larger than 1):

`L=0.25(12)^t`

`W=0.5(2.1)^t`

`f(t)=2/3(6)^t`

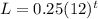
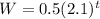
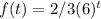
Not exponential growth or decay (no exponent):

G(x)=1.3(x)