Question

Graph the function. How is the graph a translation of f(x) = x2? y = (x –1)2 + 3

A. f(x)
translated down 3 unit(s) and translated to the right 1 unit(s)
B. f(x)
translated down 3 unit(s) and translated to the left 1 unit(s)
C. f(x)
translated up 3 unit(s) and translated to the left 1 unit(s)
D. f(x)
translated up 3 unit(s) and translated to the right 1 unit(s)

Answer 1

See pic

Explanation:

Answer 2

The correct answer is D.

EXPLANATION

The function given to us to graph is

`y=(x-1)^2+3`

This function is written in the form

`y=a(x-h)^2+k`

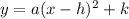
Where
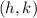`(h,k)` is the vertex.

By comparing to the given function,

`y=(x-1)^2+3`

The coordinates of the vertex are

`(1,3)`.

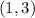Also
`a=1\:>\:0`, the graph opens up.

We also need to determine the x and y intercepts.

At x-intercept
`y=0`

`0=(x-1)^2+3`

`-3=(x-1)^2`

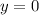
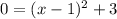
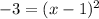
We need to take the square of both sides. But square root of negative 3 gives an imaginary number. This means the graph will be hanging. It won't touch the x-axis.

At y-intercept
`x=0`

`y=(0-1)^2+3`

`y=1+3=4`

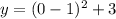
The y-intercept is
`(0,4)`.

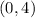We can now use the above information to graph the function as shown in the attachment.

We can see from the graph that
`y=(x-1)^2+3` is obtained when the graph of
`f(x)=x^2` is shifted up 3 units and to the right 1 unit.