Question

X-y=6
2x-3z=16
2y+z=4

Solve the systems of equations.

Answer 1

Given System of equation:

x-y =6 .....,[1]

2x-3z = 16 ......[2]

2y+z = 4 .......[3]

Rewrite the equation [1] as

y = x - 6 .......[4]

Substitute the value of [4] in [3], we get

`2(x-6)+z = 4`

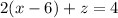
Using distributive property on LHS ( i.e,
`a \cdot (b+c) =a \cdot b+ b \cdot c` )

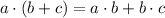then, we have

2x - 12 +z =4

Add 12 to both sides of an equation:

2x-12+z+12=4+12

Simplify:

2x +z = 16 .......[5]

On substituting equation [2] in [5] we get;

2x+z=2x -3z

or

z = -3z

Add 3z both sides of an equation:

z+3z = -3z+3z

4z = 0

Simplify:

z = 0

Substitute the value of z = 0 in [2] to solve for x;

`2x-3(0) = 16`

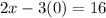
or

2x = 16

Divide by 2 both sides of an equation:

`(2x)/(2) =(16)/(2)`

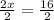
Simplify:

x= 8

Substitute the value of x =8 in equation [4] to solve for y;

y = 8-6 = 2

or

y = 2

Therefore, the solution for the given system of equation is; x = 8 , y = 2 and z =0