Answer:
a) The equation of the Parallel line to the given straight line is
6 x + y + 13 =0
b) Slope - intercept form
y = - 6 x - 13
c) The intercept - form
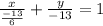
x - intercept =
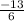
y - intercept = - 13
Explanation:
Step(i):-
Given the equation of the straight line
y = -6x +1
6 x + y - 1 = 0
The equation of the Parallel line to the given straight line is
6x + y + k=0 and it passes through the point (-3, 5 )
⇒ 6 (-3 ) + 5 + k =0
⇒ - 18 + 5 + k=0
⇒ -13 + k = 0
⇒ k = 13
The equation of the Parallel line to the given straight line is
6 x + y + 13 =0
Step(ii):-
Slope - intercept form
y = m x + C
y = - 6 x - 13
Step(iii):-
Intercept - form
6 x + y + 13 =0
6 x + y = - 13
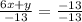
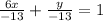
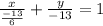
The intercept - form
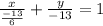
x - intercept =
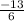
y - intercept = - 13